| Вложение | Размер |
|---|---|
| 19 КБ | |
| 53.6 КБ |
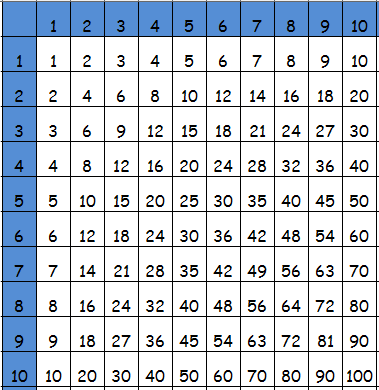
Человек часто пытается найти закономерности во всем, что его окружает, поэтому изучать умножение удобно при помощи специальной таблицы. У этой таблицы красивое название – таблица Пифагора. Также ее часто называют таблицей умножения Пифагора или просто таблицей умножения. Так она называется не только в России, но и в некоторых других странах, во Франции, Италии и др. Многие убеждены, что она названа в честь древнегреческого математика Пифагора Самосского. Сведения об этом противоречивы, более того, прототипы таблиц умножения были найдены при раскопках на месте древней Японии, Китая, Месопотамии. Так или иначе именно это название наиболее распространено сегодня. Таблица умножения Пифагора в некотором роде уникальна, она имеет ряд неоспоримых преимуществ перед таблицей с простыми столбиками примеров, которая в последнее время все чаще встречается на оборотах тетрадей по математике, у которой тоже есть некоторые свои преимущества.
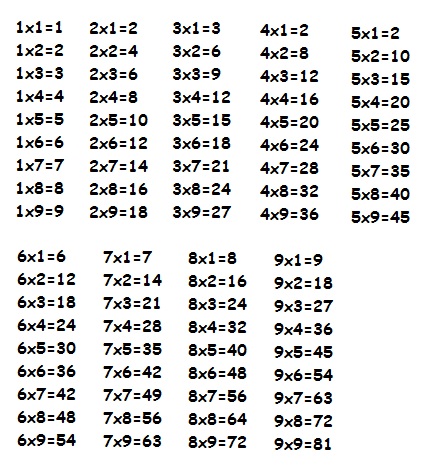
Классическая таблица умножения Пифагора выглядит следующим образом (ниже представлена картинка, если же Вам нужен файл в формате .doc для Word, то он находится в начале статьи)
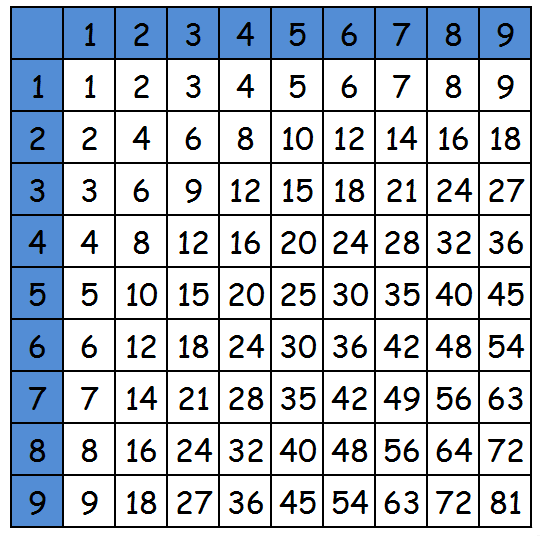
Здесь в первом столбце и первой строке указаны множители, в квадратиках – произведения. Так как умножение на 10 очень просто, то для удобства в этмо варианте нет умножения на 10. Более полный вариант с умножением на 10 можно найти в самом начале статьи, с умножением на 12 - в конце статьи. Рассмотрим на примере, как работать с таблицей. Допустим, нужно умножить 8 на 9 (8 х 9). Выбираем в первой строке цифру 8, в первом столбце цифру 9. Мысленно проводим линии до места их пересечения. Это и будет результат умножения двух чисел. Как видно из примера, все предельно просто.
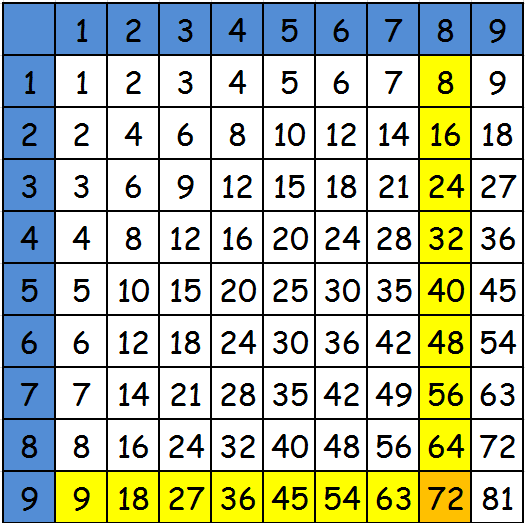
Кроме простоты таблица имеет еще ряд положительных моментов, она сама по себе интересна. Глядя на нее, легко можно найти закономерности, которые упрощают процесс запоминания. Таблица симметрична. То есть, не обязательно учить ее всю наизусть. Достаточно мысленно провести диагональ и выучить то, что находится либо над проведенной линией, либо под ней. Дальше все совсем легко. Например, мы выучили то, что находится над диагональной линией, а нужно умножить 5х4. Тогда мы меняем 5 и 4 местами и вспоминаем уже выученное значение.
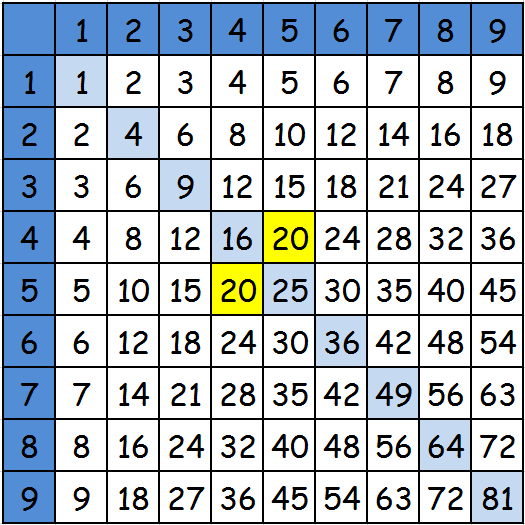
Отдельно стоит выделить еще одно свойство. Если выбрать какое-то число и провести линию вверх и в сторону до множителей, то получится прямоугольник. Причем количество клеточек в этом прямоугольнике будет равно числу, которое получится при умножении соответствующих множителей. Чтобы все было верно нужно при построении таблицы учитывать следующее правило: высота и ширина всех ячеек должна быть одинаковой (причем высота должна быть равна ширине, иначе не получится одинаковая площадь при перемене мест множителей). Рассмотрим на примере. Выбираем число 20. Проводим линию вверх и в сторону. Считаем количество полученных клеточек. Ровно 20.
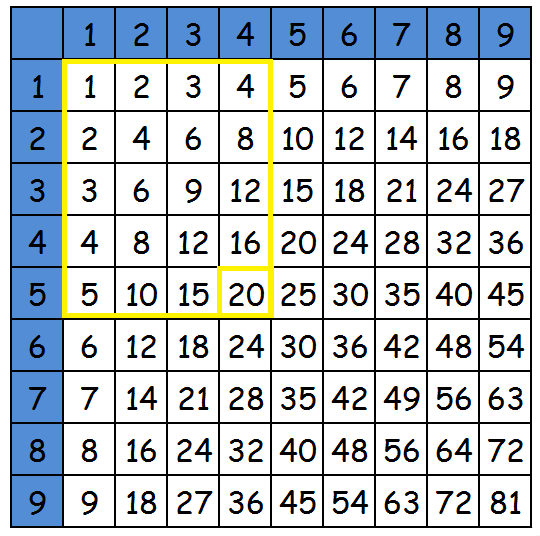
Отсюда вытекает геометрический смысл площади прямоугольника. Площадь прямоугольника равна произведению длин его сторон. Если разбирать на пальцах, то площадь прямоугольника – это и есть количество клеточек, заключенных в прямоугольнике со сторонами с определенными единичными значениями. Подводя итог, можно с сказать, что таблица Пифагора очень удобна при изучении умножения и является в какой-то степени фундаментом математики.
Также есть вариант таблицы с умножением до 12.
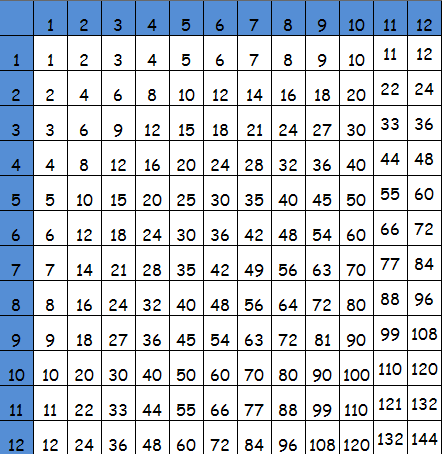
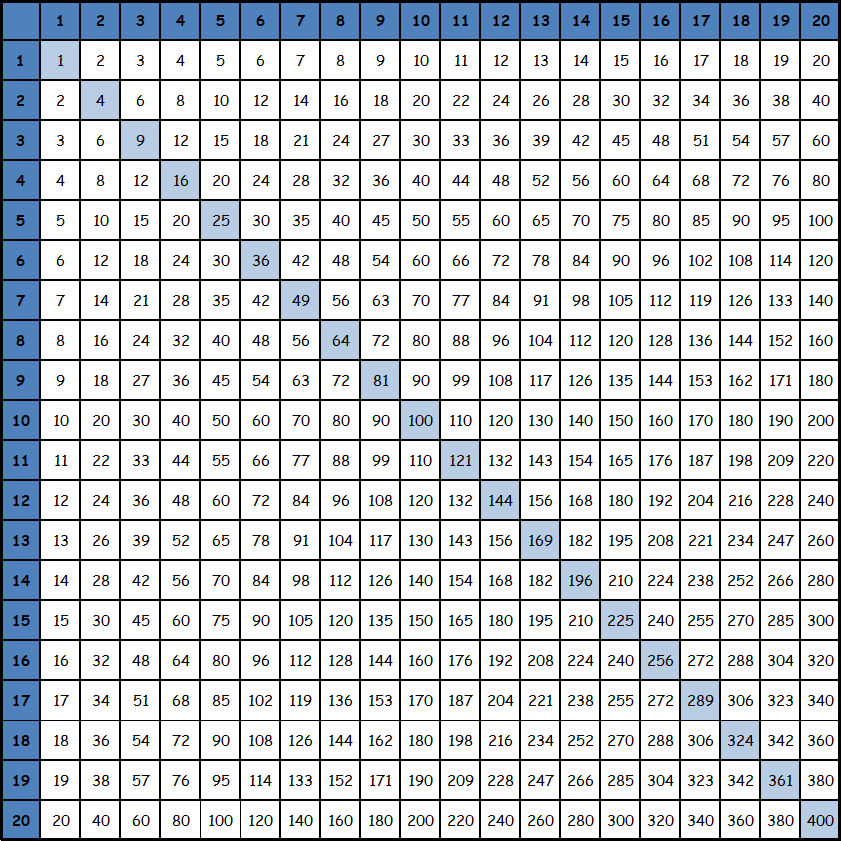
Таблица умножения Пифагора до 20.