Куб числа равен числу, возведенному в третью степень.
a3 = a · a · a
Таблица кубов.
Вариант 1.
Таблица кубов чисел от 1 до 100 (скачать и распечатат картинку или скачать и распечатать в формате .doc)
|
13 = 1 23 = 8 33 = 27 43 = 64 53 = 125 63 = 216 73 = 343 83 = 512 93 = 729 103 = 1000 |
113 = 1331 123 = 1728 133 = 2197 143 = 2744 153 = 3375 163 = 4096 173 = 4913 183 = 5832 193 = 6859 203 = 8000 |
213 = 9261 223 = 10648 233 = 12167 243 = 13824 253 = 15625 263 = 17576 273 = 19683 283 = 21952 293 = 24389 303 = 27000 |
313 = 29791 323 = 32768 333 = 35937 343 = 39304 353 = 42875 363 = 46656 373 = 50653 383 = 54872 393 = 59319 403 = 64000 |
413 = 68921 423 = 74088 433 = 79507 443 = 85184 453 = 91125 463 = 97336 473 = 103823 483 = 110592 493 = 117649 503 = 125000 |
|
513 = 132651 523 = 140608 533 = 148877 543 = 157464 553 = 166375 563 = 175616 573 = 185193 583 = 195112 593 = 205379 603 = 216000 |
613 = 226981 623 = 238328 633 = 250047 643 = 262144 653 = 274625 663 = 287496 673 = 300763 683 = 314432 693 = 328509 703 = 343000 |
713 = 357911 723 = 373248 733 = 389017 743 = 405224 753 = 421875 763 = 438976 773 = 456533 783 = 474552 793 = 493039 803 = 512000 |
813 = 531441 823 = 551368 833 = 571787 843 = 592704 853 = 614125 863 = 636056 873 = 658503 883 = 681472 893 = 704969 903 = 729000 |
913 = 753571 923 = 778688 933 = 804357 943 = 830584 953 = 857375 963 = 884736 973 = 912673 983 = 941192 993 = 970299 1003 = 1000000 |
Вариант 2.
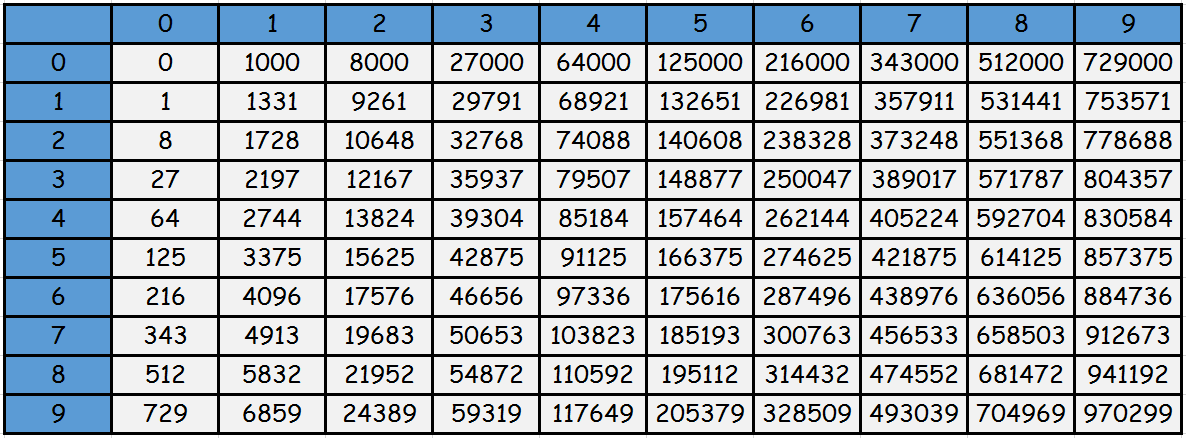
(в первом столбце указаны единицы, в первой строке - десятки, на пересечении – результат возведения числа в куб)
Скачать и распечатать картинку или скачать и распечатать doc
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 1000 | 8000 | 27000 | 64000 | 125000 | 216000 | 343000 | 512000 | 729000 |
| 1 | 1 | 1331 | 9261 | 29791 | 68921 | 132651 | 226981 | 357911 | 531441 | 753571 |
| 2 | 8 | 1728 | 10648 | 32768 | 74088 | 140608 | 238328 | 373248 | 551368 | 778688 |
| 3 | 27 | 2197 | 12167 | 35937 | 79507 | 148877 | 250047 | 389017 | 571787 | 804357 |
| 4 | 64 | 2744 | 13824 | 39304 | 85184 | 157464 | 262144 | 405224 | 592704 | 830584 |
| 5 | 125 | 3375 | 15625 | 42875 | 91125 | 166375 | 274625 | 421875 | 614125 | 857375 |
| 6 | 216 | 4096 | 17576 | 46656 | 97336 | 175616 | 287496 | 438976 | 636056 | 884736 |
| 7 | 343 | 4913 | 19683 | 50653 | 103823 | 185193 | 300763 | 456533 | 658503 | 912673 |
| 8 | 512 | 5832 | 21952 | 54872 | 110592 | 195112 | 314432 | 474552 | 681472 | 941192 |
| 9 | 729 | 6859 | 24389 | 59319 | 117649 | 205379 | 328509 | 493039 | 704969 | 970299 |
Например, чтобы найти 2 в кубе, нужно найти ячейку на пересечении строки с "2" и столбца с "0", в этой ячейке (на пересчении) будет записан результат "8".
Чтобы найти 45 в кубе, нужно найти ячейку на пересечении столбца с "4" (так как 4 дестяка) и строки с "5" (так как 5 единиц), в ней будет записан результат "91125" и т.д.
Подробнее.
Куб числа – это произведение трех одинаковых чисел, т.е. произведение трёх множителей, каждый из которых равен данному числу. Это действие также можно назвать «возведением в третью степень» (подробнее о возведении в степень можно прочитать в этой статье). Например, три в кубе записывается как «33» и с помощью этой записи обозначают следующее действие: 3х3х3. Возведение числа в третью степень является частным случаем возведения числа в степень.
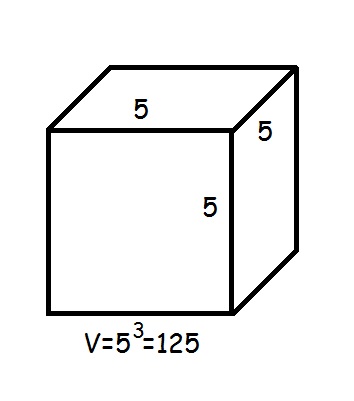
При нахождении куба получается некое значение, которое может иметь определенный геометрический смысл. Заключается он в том, что если взять куб с ребром заданной единичной длины, то объем этого куба как раз и будет равен длине ребра в третьей степени, т. е. «кубу» длины этого ребра.
Рассмотрим пример. Возьмем куб со стороной 5. Объем будет равен 53 = 125.
Для постоянных расчетов крайне неудобно пользоваться записью, представленной умножением нескольких множителей. Кроме того, намного удобнее зрительное восприятие информации. Поэтому куб чисел принято представлять в виде таблицы. По этой таблице найти искомое значение довольно просто. Ее можно распечатать и брать с собой. Часто используемые значения постепенно сами запоминаются. Таблица кубов встречается двух видов: в виде равенств, а также в виде квадратной таблицы, где в первой строке указываются десятки, в первом столбце единицы. На пересечении – результат возведения искомого числа в куб. Самой популярной является таблица, где представлено возведение в куб чисел от 1 – до 100.
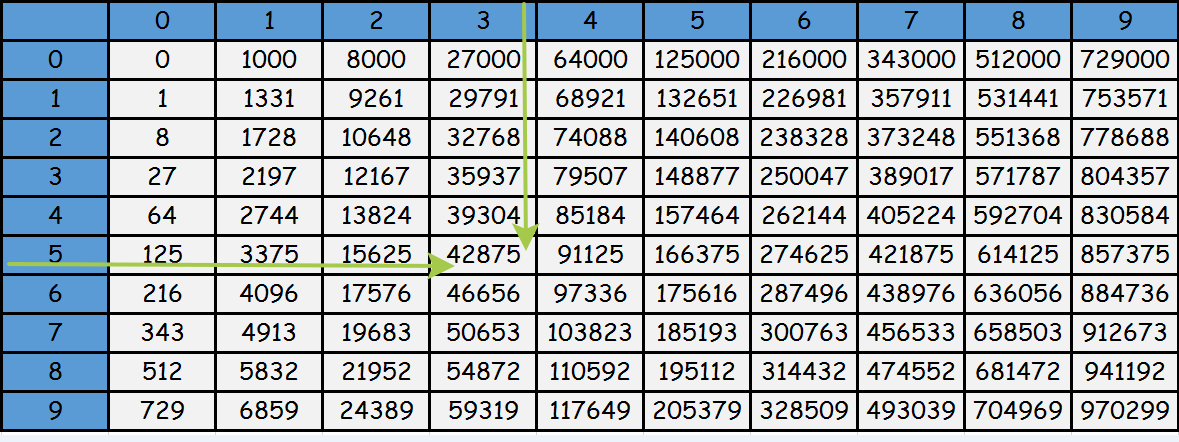
Как работать с этой таблицей? Предположим, нам нужно возвести в куб число 35. В первой строке находим цифру 3, в первом столбце – цифру 5. Проводим мысленно линии вниз и в сторону до пересечения. Это и будет искомое число 42875.
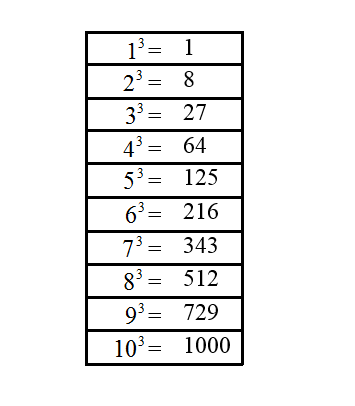
Реже встречается запись в виде равенств. Выглядит она следующим образом.
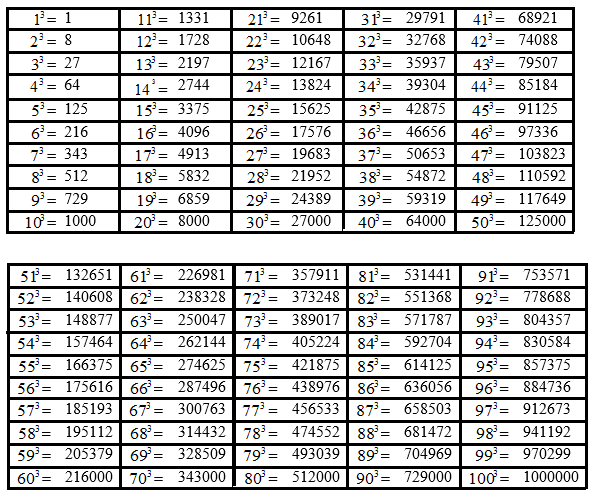
При возведении в третью степень чисел, больших ста, пользуются обыкновенным умножением числа самого на себя три раза, либо калькулятором, одной из функций которого является возведение числа в степень. Также прибегают к использованию онлайн-калькулятора или способов быстрого устного счета, абакуса и др. Результаты возведения в степень числе от 1 до 10 стараются запомнить, потому что они часто встречаются. Базовыми значениями для заучивания являются:
Чтобы возвести в куб числа с нулями в конце, совсем необязательно пользоваться таблицами. Достаточно возвести в куб впереди стоящие цифры и добавить в конце количество нулей в три раза большее, чем было в исходном числе. Например, как вычислить, сколько будет 203? Для этого возводим в куб число 2, получаем 8. Видим, что в исходном числе у нас был один ноль. Умножаем 1х3=3. Таким образом, нужно добавить три нуля. Итоговое значение 8000. Рассмотрим еще один пример. Возведем в куб число 200. Первое действие аналогично предыдущему примеру. Теперь разберемся с нулями. В исходном числе количество нулей 2, умножаем на 3, получаем 6. Таким образом, искомое значение 8000000.
